排序算法小结

0. 序言

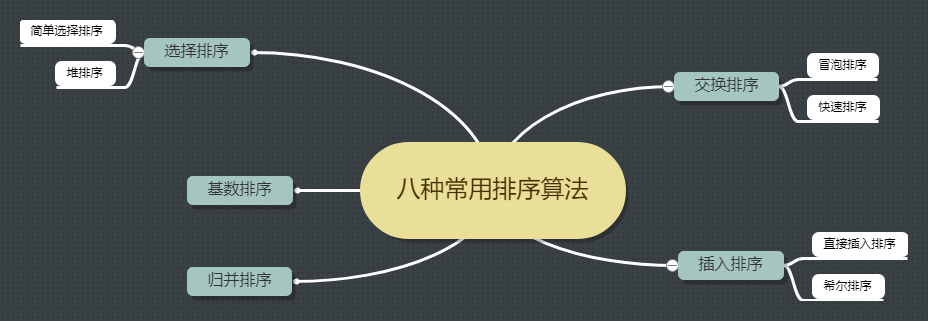
八种常见排序算法：

---

1. 冒泡排序

冒泡排序是一种较为简单的排序方法，一般说排序算法的时候都会作为第一个出现。我这种非科班出身但是学过C语言的学生必修的算法也有冒泡排序，以前听学长讲过面试的时候很可能会让你手写一个冒泡排序，所以在敲代码之外最好还要尝试手写下冒泡排序。

冒泡排序可以先这样记，冒泡排序是两层循环里面套一次比较交换（比较交换就是先比较大小，如果有需要就交换的意思）。外面一层循环是控制比较轮次的，最后一个是不需要比较的，所以是length-1轮。里面的一层循环是控制每次大循环下相邻元素的比较次数的。

冒泡排序会对相邻的两个元素依次做比较，可以看到下图，显然第一次大的循环就将最大的排到了最后面，所以下一次大的循环中是不需要对最大的元素进行操作的，以此类推，每次大循环下就将此次循环最大的元素安顿好，所以内层循环的次数是length-1-i轮。

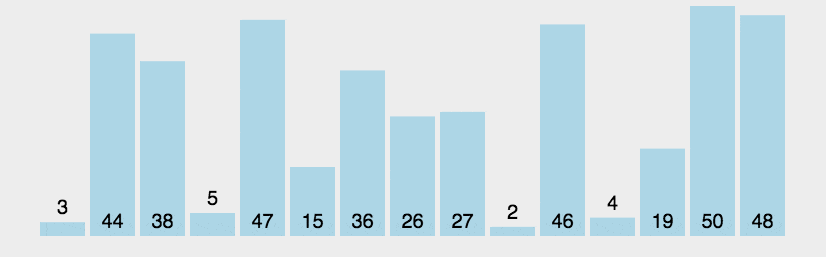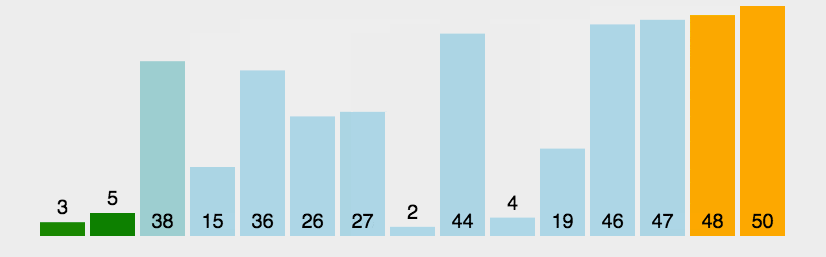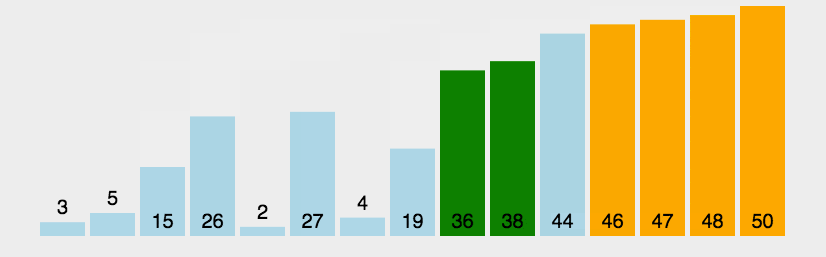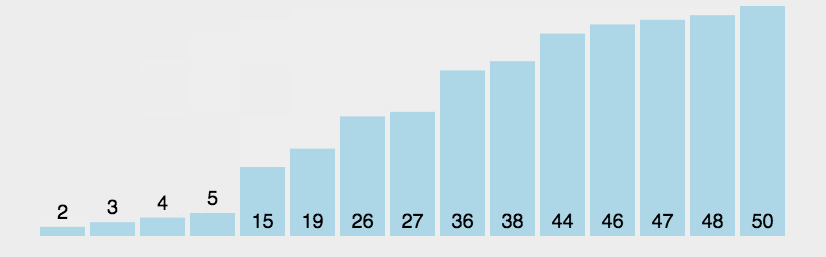
public static void bubbleSort(int[] arr){
    // 控制共比较多少轮
    // 最后一个是不需要比较的，所以是length-1轮
    for(int i=0;i<arr.length-1;i++){

        // 设定一个标记，若为true，则表示此次循环没有进行交换，也就是待排序列已经有序，排序已经完成。
        boolean flag = true;

        // 比较的次数
        for(int j =0 ;j<arr.length - i -1;j++){
            if(arr[j] > arr[j+1]){
                int tmp = arr[j];
                arr[j] = arr[j+1];
                arr[j+1] = tmp;
            }

        }

        if (flag) {
            break;
        }
    }
}

2. 插入排序

插入排序算法很像打扑克前对手牌进行排序的方法，最外面也是一层大的循环（将所有手牌全部过一遍），手上拿着你要准备换位置的牌（用个temp变量接），用这张牌比较前面排好的队列，当temp位置合适的时候插入这个位置（比它大的要向后）。

public static void insertsort(int[] arr){
    // 遍历所有的数字
    for(int i=1 ;i<arr.length;i++){

        // 如果当前数字比前一个数字小
        if(arr[i] < arr[i-1]){
            // 把当前遍历数字存起来
            int tmp = arr[i];
            int j = i-1;
            // 遍历之前的数字
            // 在之前的序列中找到合适的位置
            for( ;j>=0 && tmp< arr[j];j--){
                // 依次挪一个位置
                arr[j+1] = arr[j];
            }
// 注意Java的for循环执行顺序，此时要在arr[j+1]的位置上插入元素
            arr[j+1] = tmp;
        }

    }
}

3. 希尔排序

前面的插入排序中会遇到些极端现象，如果手上的”牌“恰巧很小而且又在靠后的位置发现，这样子会需要挪动很多的数据… 但插入排序有个优点是如果数组已经基本有序了，再去排列就会效率很高。所以诞生了希尔排序：

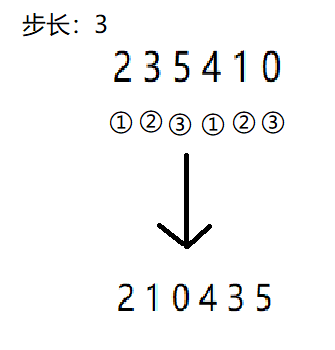
• 引入步长参数（d），步长取为总长度的一半，对数组进行分组，同一组内进行比较，如果低位的大就交换。可以发现仅通过三次，大小顺序已经有了改善。

• 如果一开始是奇数的话，最后一位还要和中间的重新比较一次，比如在这个例子最后还有一个数arr[6]，这个数在最后还需要和arr[3]再比较排序，也就是这个数也被分到第一组内了。

• 改变步长为原来的一半（d/2），重复上述行为。当然针对6个数的情况，第二次步长已经是1了。

public static void shellSort(int[] arr){
    // 遍历所有的步长
    for(int d = arr.length/2;d>0;d/=2){
        // 遍历所有的元素
        for(int i= d ;i<arr.length;i++){
            // 遍历本组中所有的元素
            for(int j = i-d;j>=0 ;j-=d){
                // 如果当前元素大于加上步长后的那个元素
                if(arr[j] > arr[j+d]){
                    int temp = arr[j];
                    arr[j] = arr[j+d];
                    arr[j+d] = temp;
                }
            }
        }
    }
}

4. 选择排序

选择排序在我看来是最简单的排序了…复杂度也是比较高的 O(n²)，唯一的好处是不需要申请额外的内存空间。

算法的步骤就是遍历数组找到最小的，排到最前面去，然后再从剩下的找第二小的…

 public static void selectsort(int[] arr) {

     // 遍历所有的数
     for(int i=0;i<arr.length;i++){
         // 最小值的索引
         int minIndex = i;
         // 把当前所有的数和后面所有的数依次进行比较，并记录下最小的数的下标
         for(int j =i+1;j<arr.length;j++){
             //
             if(arr[minIndex]>arr[j]){

                 minIndex = j;
             }
         }
// 如果minIndex的值发生了变化（找到了更小的），就交换
         if(i!=minIndex){
             int temp = arr[i];
             arr[i] = arr[minIndex];
             arr[minIndex] = temp;
         }
     }
 }

4. 快速排序

先来说实现方法，实现方法其实并不难理解。

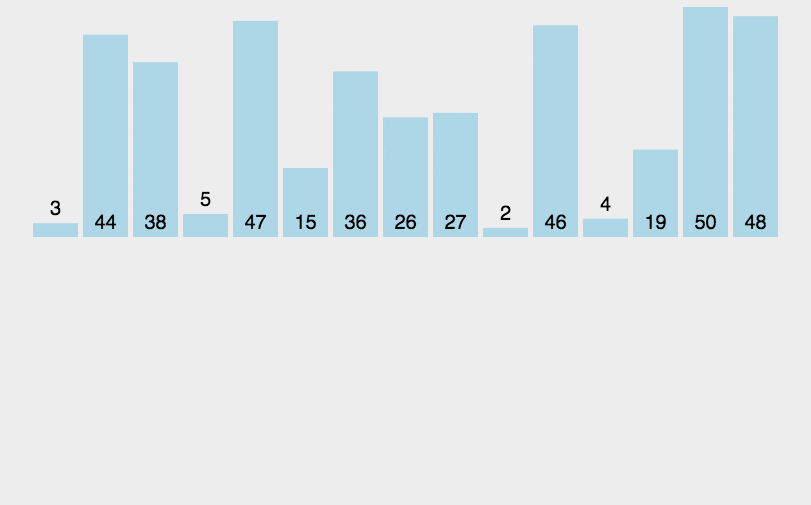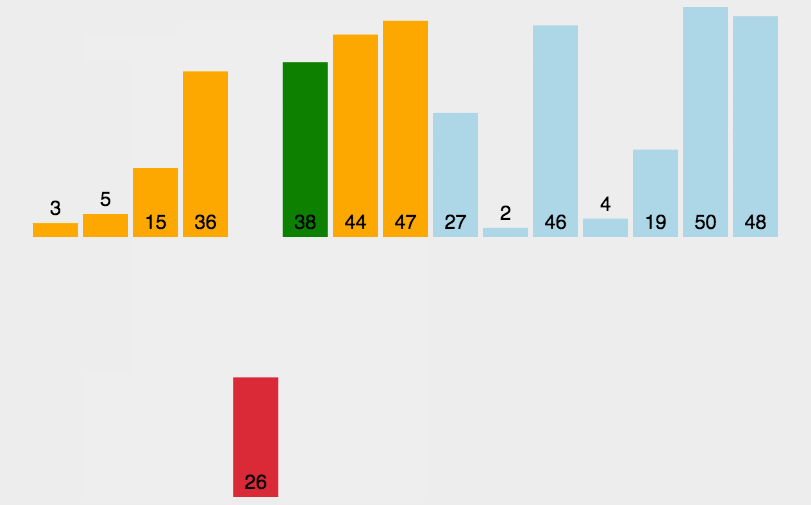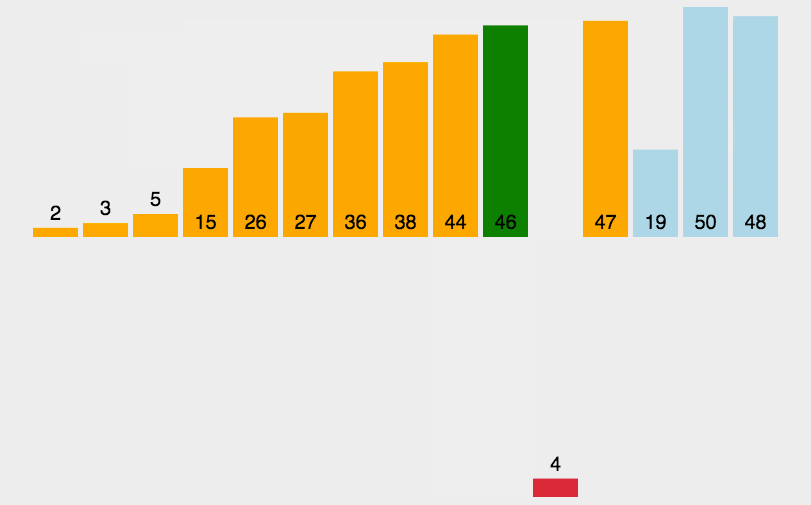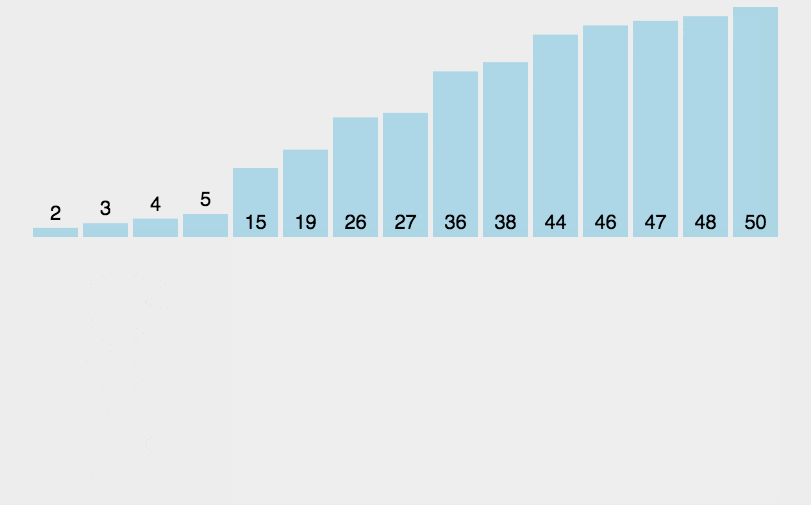
• 先找一个基准（pivot），将比基准大的数放在一侧，将比基准小的数放在另一侧。
• 再对两侧的数据分别重新找基准、重新分成两侧，以此类推。

这里蓝线就是找的基准。

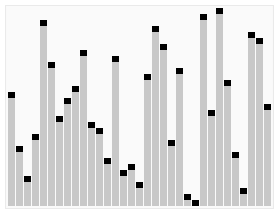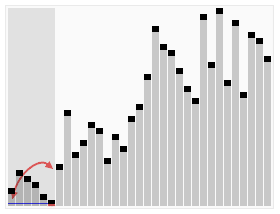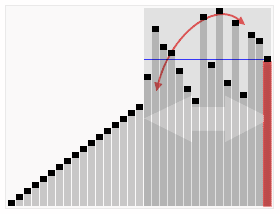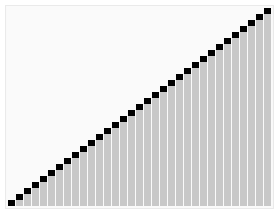
当时读到这里我的第一反应就是这个基准如何找？想到在对二分搜索树的各种优化方案中很多都是为了避免二分搜索树退化成为链表，那这里会不会每次恰巧找的基准都是最小的（最大的）呢？

这种算法本身平均情况下，算法复杂度是Ο(nlogn)，但是当出现最坏状况时，算法复杂度是O(n²)。这部分是摘抄的：

事实上，快速排序通常明显比其他 Ο(nlogn)算法更快，因为它的内部循环（inner loop）可以在大部分的架构上很有效率地被实现出来。

快速排序的最坏运行情况是 O(n²)，比如说顺序数列的快排。但它的平摊期望时间是 O(nlogn)，且 O(nlogn) 记号中隐含的常数因子很小，比复杂度稳定等于 O(nlogn)的归并排序要小很多。所以，对绝大多数顺序性较弱的随机数列而言，快速排序总是优于归并排序。

实现的具体方式如下：

• 递归函数quickSort实现：

  • 设定递归结束条件：left索引值大于right索引值；

  • 递归每一步任务：找到数组被拆分成两部分后的标记索引值，递归前一部分，递归后一部分

     // 递归函数
    private int[] quickSort(int[] arr, int left, int right) {
           // 递归结束条件
           if (left < right) {
               // 找到比基准小的部分和比基准大的部分的分界值的索引
               int partitionIndex = partition(arr, left, right);
               // 递归比之前设定的基准小的部分数组
               quickSort(arr, left, partitionIndex - 1);
               // 递归比之前设定的基准大的部分数组
               quickSort(arr, partitionIndex + 1, right);
           }
           return arr;
       }

• 数组分割函数partition实现：

  • 设定传进来的数组的第一个参数是基准值（pivot）；

  • 遍历除基准值外的数组（结束条件当然还是left索引值大于right索引值），设定一个index参数找数组分割点（其实就是一个索引值，遍历时用来记录索引，等到遍历结束后，就成为了大小两部分的分割点了，partition函数最后的返回值就是index-1），当遍历到的元素比基准值小的时候，就将index位置的元素与遍历的元素交换，index前进一步。

       // partition()函数实现的功能就是将数组分成两部分，一部分比基准大，一部分比基准小，最后返回两部分分割点的索引值。
    private int partition(int[] arr, int left, int right) {
           // 设定基准值（pivot）
           int pivot = left;
           int index = pivot + 1;
           for (int i = index; i <= right; i++) {
               if (arr[i] < arr[pivot]) {
                   // 将比索引值小的元素放到较前面的位置上
                   swap(arr, i, index);
                   index++;
               }
           }
           // 基准值放到分割点上
           swap(arr, pivot, index - 1);
           // 最后作为大小两部分的分割点的索引
           return index - 1;
       }

以上就是快排的实现方法，快排顾名思义就是比较快速的排序方法，实际中使用的也较多。

5. 归并排序